Skip to contents

Analysis of CO2 data with Gaussian Processes

time_series_analysis.Rmd

Learner Outcomes:

This vignette demonstrates a simplified version of the Mauna Loa case study presented by Rasmussen and Williams (2006, 119–21), using zoomerGP. The analysis involves fitting an additive GP model to co2 data collected at the Mauna Loa Observatory from from 1959 to 1997. The data are included with R in the co2 dataset.

After completing the vignette, you should be able to:

  1. Be able to write and fit a basic GP model with Empirical Bayes using zoomerGP
  2. Extract predictions from this model and plot them
  3. Use zoomerGP to generate predictions from sub-components of the model and examine them

Getting Started: Setup and Data Processing

First, we load the libraries we will use for data analysis (zoomerGP for fitting the GP models and ggplot2 for plotting the raw data). We then transform the built-in co2 dataset to a tidy dataframe with one row per observation.

library(zoomerGP)
library(ggplot2)

data <- data.frame(
  year = (1:length(co2) - 1)/12 + 1959,
  co2 = c(co2)
)

head(data)
#>       year    co2
#> 1 1959.000 315.42
#> 2 1959.083 316.31
#> 3 1959.167 316.50
#> 4 1959.250 317.56
#> 5 1959.333 318.13
#> 6 1959.417 318.00

Using ggplot2, we can then plot the raw data:

ggplot(data, aes(x=year, y=co2)) +
  geom_point() + 
  theme_bw() + 
  xlab("Year") + 
  ylab("co2 concentration (parts per million)")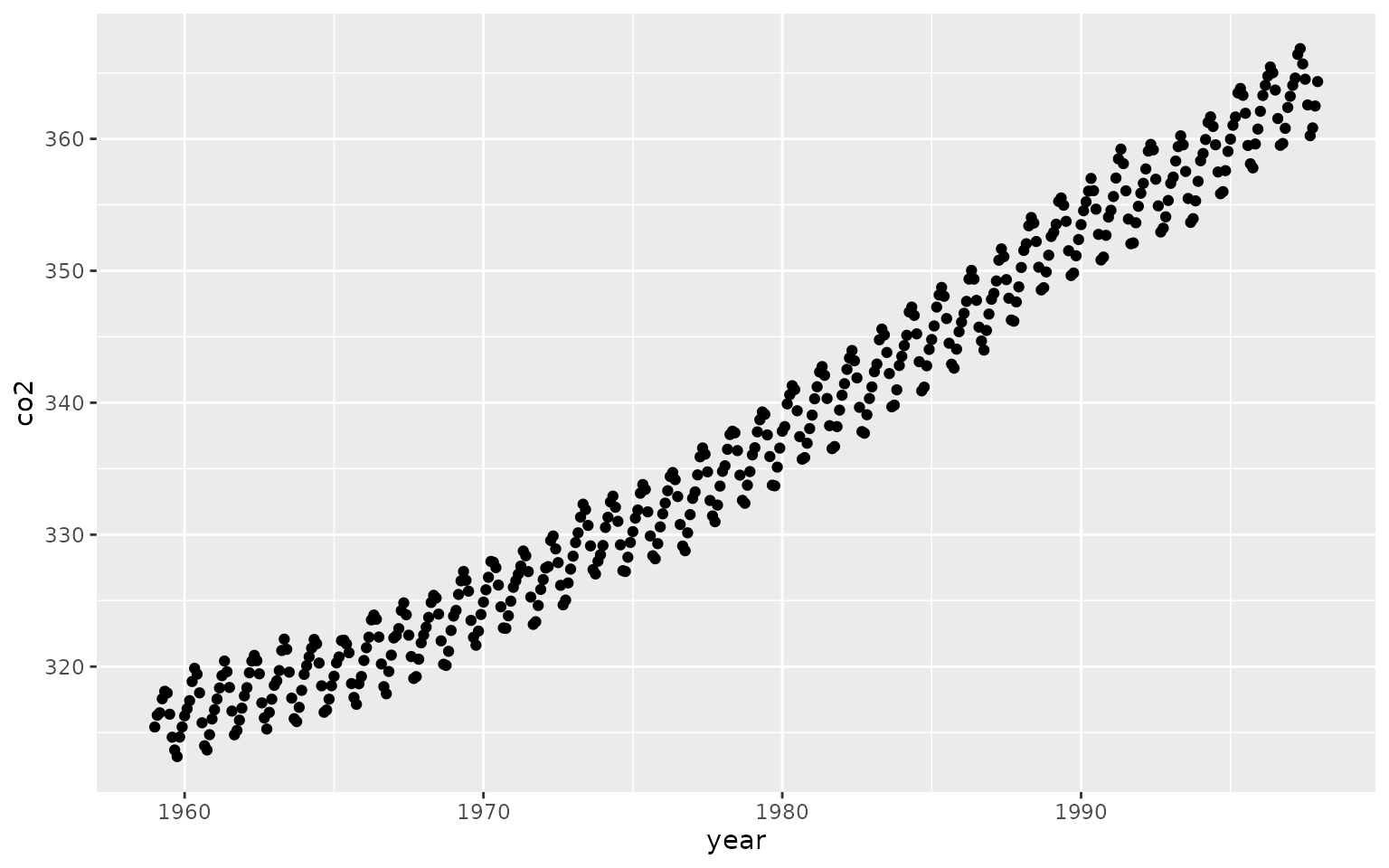

## Specifying and Fitting the Model

The data appear to be reflective of a long-term process combined with a seasonal process which repeats every 12 months. This motivates a simplified version of the model described by Rassmusen and Williams (2005), which describes the co2 concentration observed at a given time (yi)(y_i) as follows:

yi=α+f1(t)+f2(t)+εi y_i = \alpha + f_1(t) + f_2(t) + \varepsilon_i

Where α\alpha is an intercept term, and εi\varepsilon_i is a noise term. f1f_1 and f2f_2 are mean-zero Gaussian processes that absorb the long-term and periodic components, respectively. Specifically, we parameterize the kernels as described below. The formulas for the RBF and Periodic kernels are are taken from Bayesian Data Analysis, 3rd edition (Gelman et al. 2021, 515).

  • f1f_1 absorbs the long-term trend and is parameterized with an RBF kernel: f1∼GP(0,k1),k2(t,t′)=σ12exp(−(t−t′)22l12)f_1 \sim GP(0, k_1), \quad k_2(t,t') = \sigma_1^2 \exp{\bigg(-\frac{(t-t')^2}{2l_1^2}\bigg)}
  • f2f_2 absorbs the periodic trend, and is parameterized by an RBF kernel multiplied by a periodic kernel with a period of one year: f2∼GP(0,k2),k2(t,t′)=σ22exp(−(t−t′)22l22)σ32exp(−sin2(π(t−t′))l32)f_2 \sim GP(0, k_2), \quad k_2(t,t') = \sigma_2^2 \exp{\bigg(-\frac{(t-t')^2}{2l_2^2}\bigg)} \sigma_3^2 \exp{\bigg(-\frac{\sin^2(\pi (t-t'))}{l_3^2}\bigg)}. The inclusion of the RBF kernel allows for the periodic component to change slightly over time.

zoomerGP provides a convenient formula syntax to describe this model, which we then fit using Empirical Bayes.

set.seed(1)
gp_model <- gaussian_process(
  co2 ~ periodic(year, periods = c(1.0))*rbf(year) + rbf(year), 
  data = data, 
  sparse = F, 
  )
gp_model
#> A Gaussian Process model with 468 observations
#> Log-Likelihood: -281.155936
#> R-Squared: 0.999801
#> Kernel Specification:
#> └──  (A) Plus (+)
#>     ├──  (AA) Times (*)
#>     │   ├──  (AAA) Periodic Kernel
#>     │   └──  (AAB) RBF Kernel
#>     └──  (AB) RBF Kernel

Examining the model fit object, we can see the log-likelihood, r-squared and.

prediction_data <- data.frame(year = 1959 + seq(0,90, length.out = 500))
prediction_data$preds <- predict(gp_model, prediction_data)[,1]
prediction_data$pred_var <- predict(gp_model, prediction_data)[,3]

prediction_data$ci_lo <- prediction_data$preds + 2*sqrt(prediction_data$pred_var)
prediction_data$ci_hi <- prediction_data$preds - 2*sqrt(prediction_data$pred_var)

ggplot() + 
  geom_point(data = data, aes(x=year, y=co2)) + 
  geom_line(data = prediction_data, aes(x=year, y=preds)) + 
  geom_line(data = prediction_data, aes(x=year, y=ci_hi), linetype = 2, col = "darkgrey") + 
  geom_line(data = prediction_data, aes(x=year, y=ci_lo), linetype = 2, col = "darkgrey")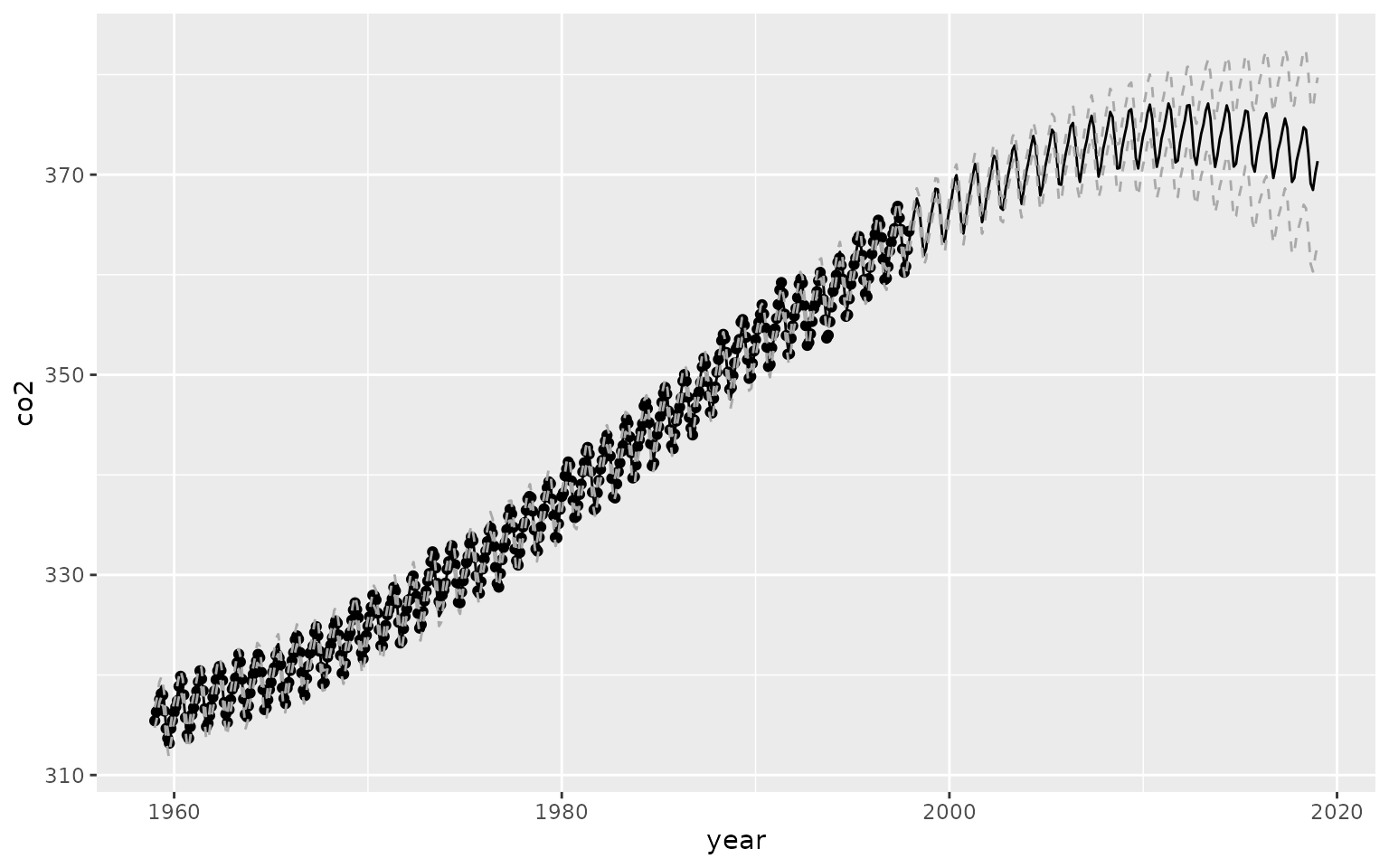

If we want to extract the periodic component, we can easily do so by isolating the “”

Gelman, Andrew, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin. 2021. Bayesian Data Analysis. 3rd ed. Chapman; Hall/CRC. https://sites.stat.columbia.edu/gelman/book/BDA3.pdf.
Rasmussen, Carl Edward, and Christopher K. I. Williams. 2006. Gaussian Processes for Machine Learning. The MIT Press.